数学のコツ 〜関数 \(y = ax^2\)〜
中学3年では2次方程式が終わると\(y = ax^2\)という形の関数を習います。中2で習った1次関数に比べて少し複雑な関数で、もちろんグラフの形も異なります。中学の数学もここまでくると結構難しくなるので注意が必要です。というわけで、今日は\(y = ax^2\)のコツを紹介します!
1. 1次関数と混乱しないで!
中2で習う1次間数は
$$ y = ax + b $$
という式で表されました。それぞれ\(a\)と\(b\)の部分に具体的な数値が入り、ひとつの直線を表す式になります。では改めて次の関数を見てみましょう
$$ y = ax^2 $$
こちらでも1次関数と同じように\(a\)というパラメータが出てきます。1次関数と同じ様な値なんだな〜…と思った人は要注意です!実はこの\(a\)は1次関数の\(a\)とはちょっと意味が違います。
1次関数の\(a\)は傾きというパラメータで関数の変化の割合を表します。1次関数はこの変化の割合が常に一定なので直線を表す式になります。
それに対して\(y = ax^2\)はご存知の通り曲線を表す関数になります。なので変化の割合は常に一定ではなく、着目する区間により変わってしまいます。
では\(y = ax^2\)の\(a\)は何を表すのでしょうか?
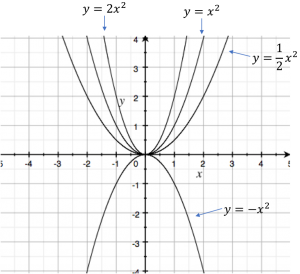
実はこの\(a\)は関数自体の形を表すパラメータとなります。\(a\)の値が正の値ならグラフは下に凸、負の値なら上に凸。\(a\)が0から離れるほどグラフは急峻な形となり、0に近づくほどなだらかな形となります。
同じ\(a\)では違う役割があるので注意してください!
2. 最大値と最小値を考えよう
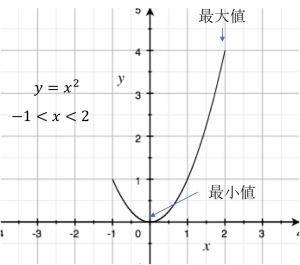
1次関数は直線なので、\(x\)の変域が決まると最大値と最小値は必ず変域の両側に表れました。
しかしながら\(y = ax^2\)の関数は直線ではなく放物線となるため、必ずしも最大値と最小値が変域の両側に表れるとは限りません!
どういうことかというと、変域が0をまたいで設定されているときは関数の凸の部分が含まれるので要注意です。\(y = ax^2\)の\(a\)の値に応じて、関数がどちらに凸かを考えて、最大値と最小値を慎重に考えてみましょう!
3. 直線との交点は?
1次関数を習ったとき、2つの直線の交点を求める問題がよく出たと思います。どのように解いたかというと、2つの1次関数の式を連立方程式として答えを求めたと思います。
では\(y = ax^2\)と1次関数\(y=ax+b\)の交点はどのように求めるのでしょうか?
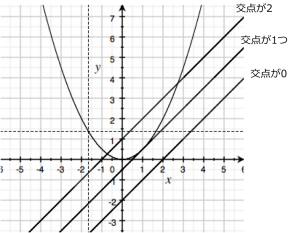
こちらも同様に連立方程式として求めることが出来ます。1次関数\(y=ax+b\)をそのまま\(y = ax^2\)の\(y\)の値に代入すると\(x\)の2次方程式になると思います。この形になったら、後は因数分解や解の公式で交点を求めることが出来ます。
しかしこのとき一つだけ注意点があります。それは1次関数と2次関数の場合、交点の数が異なる場合があります。交点が2つの場合、1つの場合、無い場合と分かれるので注意してください。
科目: 英語・数学
月額: 15,000~ (1教科, 1回80分, 月4回の場合)
☆科目、授業回数などご希望があれば臨機応変に対応します
自習スペース: 1日最大500円で利用可能
tel: 03-6453-4545
mail: info@soraoto.net
web: http://www.soraoto-kobetsu.net