数学のコツ 〜三平方の定理〜
中学3年で習う三平方の定理、通称ピタゴラスの定理。図形が苦手な人はよりわからなくなってしまう分野だと思います。そこで今日は三平方の定理のコツを紹介します!
1. 三平方の定理って何が出来るの?
まずは始めに三平方の定理を確認しておきましょう。三平方の定理とは直角三角形の3辺の長さの関係を表した定理で、次の図と式の関係が成り立ちます。
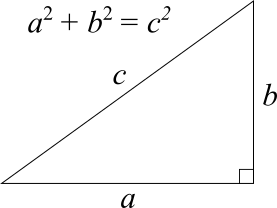
この式が何を意味するかというと、直角三角形の3つの辺の内、2つの長さがわかればもうひとつの辺の長さがわかるということです。したがって三平方の定理の問題は、わからない辺の長さを求めたり、その長さを活用して図形の面積を求めたりする問題が多くなります。まずはこの点をしっかり覚えておきましょう。
2. 一番長い辺を探そう
では次に三平方の定理を使って問題を解く際、どのように考えるか、式を見ながら考えてみましょう。
$$ a^2 + b^2 = c^2 $$
この式は直角三角形の短い2辺をそれぞれ2乗して足し算した値が一番長い辺の2乗した値と等しいということを表しています。なので、まずは直角三角形の一番長い辺を見つけるようにすると間違いが少なくなります。
直角三角形では、直角である角のちょうど対角線上の辺が、最も長い変となります。問題が出たらまずは自分が見やすい方向に直角三角形を回転させて、一番長い辺をみつけましょう。あとはシンプルに辺の長さを式に当てはめれば自動的に解くことが出来ます。
3. よくでる形は覚えよう
三平方の定理は上で書いたように直角三角形の3辺の長さに関する法則ですが、次のような角度との関係を表す図形もよく出てきます。
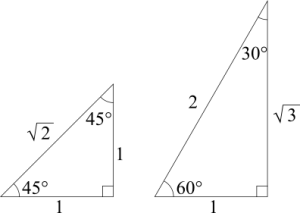
直角以外の2角がそれぞれ45°のとき、3辺の比は\(1:1:\sqrt{2}\)。直角以外の2角がそれぞれ30°と60°のとき、3辺の比は\(1:2:\sqrt{3}\)となります。
この直角三角形の3辺の比と角度の関係はとてもよくでてきますので、覚えてしまいましょう!問題を解いている時、この角度や比が出たらすぐこの三角形を思い出せるようにしておくと役立つと思います。
三平方の定理は四角形や円と組み合わせた問題がよく見られます。一見複雑そうに見えますが、基本を覚えておけばそれほど難しくありません。ぜひ色んな問題を解いてみてください!
科目: 英語・数学
月額: 15,000~ (1教科, 1回80分, 月4回の場合)
☆科目、授業回数などご希望があれば臨機応変に対応します
自習スペース: 1日最大500円で利用可能
tel: 03-6453-4545
mail: info@soraoto.net
web: http://www.soraoto-kobetsu.net
